第 4 章进阶技巧

程序的可读性和执行效率是两个很重要的要求.这一章主要介绍如何提高这两点.

4.1 apply函数族

apply并不能提高执行效率,只能使代码简洁易读.

详细的介绍可以在apply函数族介绍查看,其中给了一些简单的例子.下面演示一下稍微复杂的用法.

对矩阵按列进行操作,每列的奇数项求和,偶数项求和:

m <- matrix(1:12,4,3)
m

##      [,1] [,2] [,3]
## [1,]    1    5    9
## [2,]    2    6   10
## [3,]    3    7   11
## [4,]    4    8   12

apply(m, 2, tapply,rep(1:2,2), sum)

##   [,1] [,2] [,3]
## 1    4   12   20
## 2    6   14   22

对矩阵按列进行操作,每列前两项求和,后两项求和:

apply(m, 2, tapply,rep(1:2,each=2), sum)

##   [,1] [,2] [,3]
## 1    3   11   19
## 2    7   15   23

下面看一个3维情况的例子.

a <- array(1:24,dim = c(2,3,4))
a

## , , 1
## 
##      [,1] [,2] [,3]
## [1,]    1    3    5
## [2,]    2    4    6
## 
## , , 2
## 
##      [,1] [,2] [,3]
## [1,]    7    9   11
## [2,]    8   10   12
## 
## , , 3
## 
##      [,1] [,2] [,3]
## [1,]   13   15   17
## [2,]   14   16   18
## 
## , , 4
## 
##      [,1] [,2] [,3]
## [1,]   19   21   23
## [2,]   20   22   24

固定1个维度,对另外2个维度求和:

apply(a,1,sum)

## [1] 144 156

这样看起来不太直观,我们利用aperm函数调整数组的维度顺序:

aperm(a,c(2,3,1))

## , , 1
## 
##      [,1] [,2] [,3] [,4]
## [1,]    1    7   13   19
## [2,]    3    9   15   21
## [3,]    5   11   17   23
## 
## , , 2
## 
##      [,1] [,2] [,3] [,4]
## [1,]    2    8   14   20
## [2,]    4   10   16   22
## [3,]    6   12   18   24

固定2个维度,对1个维度求和:

apply(a,c(2,3),sum)

##      [,1] [,2] [,3] [,4]
## [1,]    3   15   27   39
## [2,]    7   19   31   43
## [3,]   11   23   35   47

固定2个维度,对1个维度分组求和:

apply(a,c(1,2),tapply,rep(c(-1,-2),2), sum)

## , , 1
## 
##    [,1] [,2]
## -2   26   28
## -1   14   16
## 
## , , 2
## 
##    [,1] [,2]
## -2   30   32
## -1   18   20
## 
## , , 3
## 
##    [,1] [,2]
## -2   34   36
## -1   22   24

对第三个维度奇数项、偶数项分别求和(奇数项是-1组,偶数项是-2组).

4.2 并行

单次模拟时间越长,重复次数越多,并行得到的提升越明显.

R中有很多并行包,可以在不同并行包比较查看对比.

这里介绍的foreach是比较友好的一个包.

下面以线性模型估计系数为例,给出示例代码.

sim_single可以在单次估计程序查看.其中SLP参数用于增加单次模拟的计算量(运行时间).

4.2.1 低重复次数,低计算量

source("code/parallel-demo.R")
library("foreach")
library("doParallel")
beta0 = c(1,-2,3)
N = c(50,100,200)
distribution= c(rnorm,rcauchy)
SIM = 500
tstart=Sys.time()
cl <- makeCluster(detectCores())
registerDoParallel(cl)
result <- foreach(n=N,.combine = rbind) %:%
  foreach(dst=distribution,.combine = c) %:%
  foreach(i=1:SIM,.combine = '+',
          .packages = c("MASS") )%dopar%{
            sim_single(n,beta0,SLP=FALSE,mydist = dst)
          }
stopImplicitCluster()
t.end=Sys.time()
t.end-tstart

## Time difference of 2.182 secs

result/SIM

##            [,1]   [,2]  [,3]     [,4]   [,5]  [,6]
## result.1 0.9988 -2.006 3.002 -0.05712 -1.969 1.962
## result.2 0.9979 -1.996 2.997  2.41988 -4.019 1.518
## result.3 0.9985 -2.002 3.007  0.62494 -2.432 2.903

把申请cluster的命令去掉,%dopar%换成%do%程序就会按串行执行

source("code/parallel-demo.R")
library("foreach")
library("doParallel")
beta0 =  c(1,-2,3)
N = c(50,100,200)
distribution= c(rnorm,rcauchy)
SIM = 500
tstart=Sys.time()
#cl <- makeCluster(detectCores())
#registerDoParallel(cl)
result <- foreach(n=N,.combine = rbind) %:%
  foreach(dst=distribution,.combine = c) %:%
  foreach(i=1:SIM,.combine = '+',
          .packages = c("MASS") )%do%{
            sim_single(n,beta0,SLP=FALSE,mydist = dst)
          }
#stopImplicitCluster()
t.end=Sys.time()
t.end-tstart

## Time difference of 2.285 secs

result/SIM

##            [,1]   [,2]  [,3]    [,4]    [,5]    [,6]
## result.1 1.0005 -1.997 3.003  7.4661 -4.5211 -0.2274
## result.2 0.9939 -2.002 3.003 -0.8143 -0.4892  4.1754
## result.3 1.0036 -2.002 2.996  0.4728 -1.9347  0.9797

4.2.2 高重复次数,低计算量

增加到1000次.

并行:

source("/Users/wang/Documents/GitHub/Simulation-in-R/code/parallel-demo.R")
library("foreach")
library("doParallel")
beta0 = c(1,-2,3)
N = c(50,100,200)
distribution= c(rnorm,rcauchy)
SIM = 1000
tstart=Sys.time()
cl <- makeCluster(detectCores())
registerDoParallel(cl)
result <- foreach(n=N,.combine = rbind) %:%
  foreach(dst=distribution,.combine = c) %:%
  foreach(i=1:SIM,.combine = '+',
          .packages = c("MASS") )%dopar%{
            sim_single(n,beta0,SLP=FALSE,mydist = dst)
          }
stopImplicitCluster()
t.end=Sys.time()
t.end-tstart

## Time difference of 3.403 secs

result/SIM

##           [,1]   [,2]  [,3]   [,4]   [,5]  [,6]
## result.1 1.007 -2.013 2.999 0.1556 -2.407 3.176
## result.2 1.008 -2.002 2.996 0.7327 -2.565 3.577
## result.3 1.000 -2.000 2.997 2.5792 -2.113 2.966

串行:

source("code/parallel-demo.R")
library("foreach")
library("doParallel")
beta0 =  c(1,-2,3)
N = c(50,100,200)
distribution= c(rnorm,rcauchy)
SIM = 1000
tstart=Sys.time()
#cl <- makeCluster(detectCores())
#registerDoParallel(cl)
result <- foreach(n=N,.combine = rbind) %:%
  foreach(dst=distribution,.combine = c) %:%
  foreach(i=1:SIM,.combine = '+',
          .packages = c("MASS") )%do%{
            sim_single(n,beta0,SLP=FALSE,mydist = dst)
          }
#stopImplicitCluster()
t.end=Sys.time()
t.end-tstart

## Time difference of 4.604 secs

result/SIM

##            [,1]   [,2]  [,3]   [,4]    [,5]  [,6]
## result.1 1.0017 -1.999 3.000 1.5062 -2.2061 2.577
## result.2 1.0032 -1.990 2.997 3.9836 -0.5012 3.743
## result.3 0.9991 -1.997 2.997 0.8568 -2.0615 2.718

4.2.3 低重复次数,高计算量

增加每次模拟的计算量,延长单次模拟的时间.

并行:

source("/Users/wang/Documents/GitHub/Simulation-in-R/code/parallel-demo.R")
library("foreach")
library("doParallel")
beta0 = c(1,-2,3)
N = c(50,100,200)
distribution= c(rnorm,rcauchy)
SIM = 500
tstart=Sys.time()
cl <- makeCluster(detectCores())
registerDoParallel(cl)
result <- foreach(n=N,.combine = rbind) %:%
  foreach(dst=distribution,.combine = c) %:%
  foreach(i=1:SIM,.combine = '+',
          .packages = c("MASS") )%dopar%{
            sim_single(n,beta0,SLP=TRUE,mydist = dst)
          }
stopImplicitCluster()
t.end=Sys.time()
t.end-tstart

## Time difference of 9.387 secs

result/SIM

##            [,1]   [,2]  [,3]  [,4]   [,5]  [,6]
## result.1 1.0101 -2.001 2.994 1.373 -1.572 2.844
## result.2 0.9968 -2.013 2.992 3.813 -4.572 8.934
## result.3 0.9996 -1.997 3.000 7.350 -4.860 3.662

串行:

source("code/parallel-demo.R")
library("foreach")
library("doParallel")
beta0 =  c(1,-2,3)
N = c(50,100,200)
distribution= c(rnorm,rcauchy)
SIM = 500
tstart=Sys.time()
#cl <- makeCluster(detectCores())
#registerDoParallel(cl)
result <- foreach(n=N,.combine = rbind) %:%
  foreach(dst=distribution,.combine = c) %:%
  foreach(i=1:SIM,.combine = '+',
          .packages = c("MASS") )%do%{
            sim_single(n,beta0,SLP=TRUE,mydist = dst)
          }
#stopImplicitCluster()
t.end=Sys.time()
t.end-tstart

## Time difference of 38.65 secs

result/SIM

##            [,1]   [,2]  [,3]    [,4]    [,5]    [,6]
## result.1 1.0086 -2.010 2.998 12.4454 -0.4945 0.05709
## result.2 0.9932 -1.998 2.997 -0.6948 -3.1508 1.68111
## result.3 0.9986 -2.003 3.001  0.8107 -1.7691 3.49674

4.2.4 模型选择

除了蒙特卡洛模拟之外,另外一个很适合并行的应用是模型选择.下面的例子用AIC对线性模型进行选择:

AIClm <- function(Y,X,ind){#单次计算AIC,ind为纳入模型的变量下标
  AIC(lm(Y~X[,ind]))
}
gen_ind <- function(bt, index) bt*index#生成候选模型下标

n = 100
p = 18
m0 = p%/%3
p0 = sample(1:p,m0)
beta = rep(0,p)
beta[p0] = 1:2
X <- matrix(rnorm(n*p),n,p)
Y <- X%*%beta + rnorm(n)

##生成所有候选模型的下标
pl <- 1:(2^p - 1)
mt <- matrix(0,2^p-1,p)
for (i in pl) {
  mt[i,]=rev(as.integer(intToBits(i)[1:(p)] ))
}
index = 1:p
lst = t(apply(mt, 1, gen_ind,index=index))

#并行
library("foreach")
library("doParallel")
tstart=Sys.time()
cl <- makeCluster(detectCores())
registerDoParallel(cl)
foreach(i=1:(2^p-1),.combine = c) %dopar%{
  AIClm(Y,X,lst[i,])
}->result
stopImplicitCluster()
t.end=Sys.time()
t.end-tstart

## Time difference of 1.405 mins

which(lst[which.min(result),]!=0)

##  [1]  1  5  6  8 11 12 13 15 16 17 18

which(beta!=0)

## [1]  6  8 13 16 17 18

#串行
tstart=Sys.time()
cl <- makeCluster(detectCores())
registerDoParallel(cl)
foreach(i=1:(2^p-1),.combine = c) %do%{
  AIClm(Y,X,lst[i,])
}->result
stopImplicitCluster()
t.end=Sys.time()
t.end-tstart

## Time difference of 3.495 mins

which(lst[which.min(result),]!=0)

##  [1]  1  5  6  8 11 12 13 15 16 17 18

which(beta!=0)

## [1]  6  8 13 16 17 18

4.3 Rcpp

Rcpp提供了R与C++的无缝接口,可以很方便的在R中调用编写的C++程序.

Rcpp文档

如何改写R程序

Rcpp已提供的分布函数

可以通过cppFunction直接在R中编写:

Rcpp::cppFunction('int add(int x, int y, int z) {
  int sum = x + y + z;
  return sum;
}')
add

## function (x, y, z) 
## .Call(<pointer: 0x10af678f0>, x, y, z)

add(1, 2, 3)

## [1] 6

但是这种方式在编写(没有语法高亮)、调试(定位编译报错行号)时都有不便.推荐单独编写cpp文件,通过sourceCpp加载.

下面以矩阵按列求和为例,比较col_mean(自己编写的C++函数)¹¹、colMeans(R base中提供的注重速度的函数)、mean_R(在R中用编写的函数)以及apply的运行速度.

Rcpp::sourceCpp('code/Rcpp-demo.cpp')

## 
## > mean_R <- function(X) {
## +     n = dim(X)[1]
## +     m = dim(X)[2]
## +     cm <- rep(0, m)
## +     for (i in 1:n) {
## +         cm = cm + X[i, ]
## +     }
## +    .... [TRUNCATED]

m = 200
n = 100
X <- matrix(rnorm(m*n),m,n)
col_mean(X) -> l1
mean_R(X) -> l2
all.equal(l1,l2)

## [1] TRUE

colMeans(X) -> l3
all.equal(l1,l3)

## [1] TRUE

apply(X, 2, mean) -> l4
all.equal(l1,l4)

## [1] TRUE

bench::mark(
  col_mean(X),
  colMeans(X),
  mean_R(X),
  apply(X, 2, mean),
  check = FALSE,relative = TRUE
)->results
ggplot2::autoplot(results)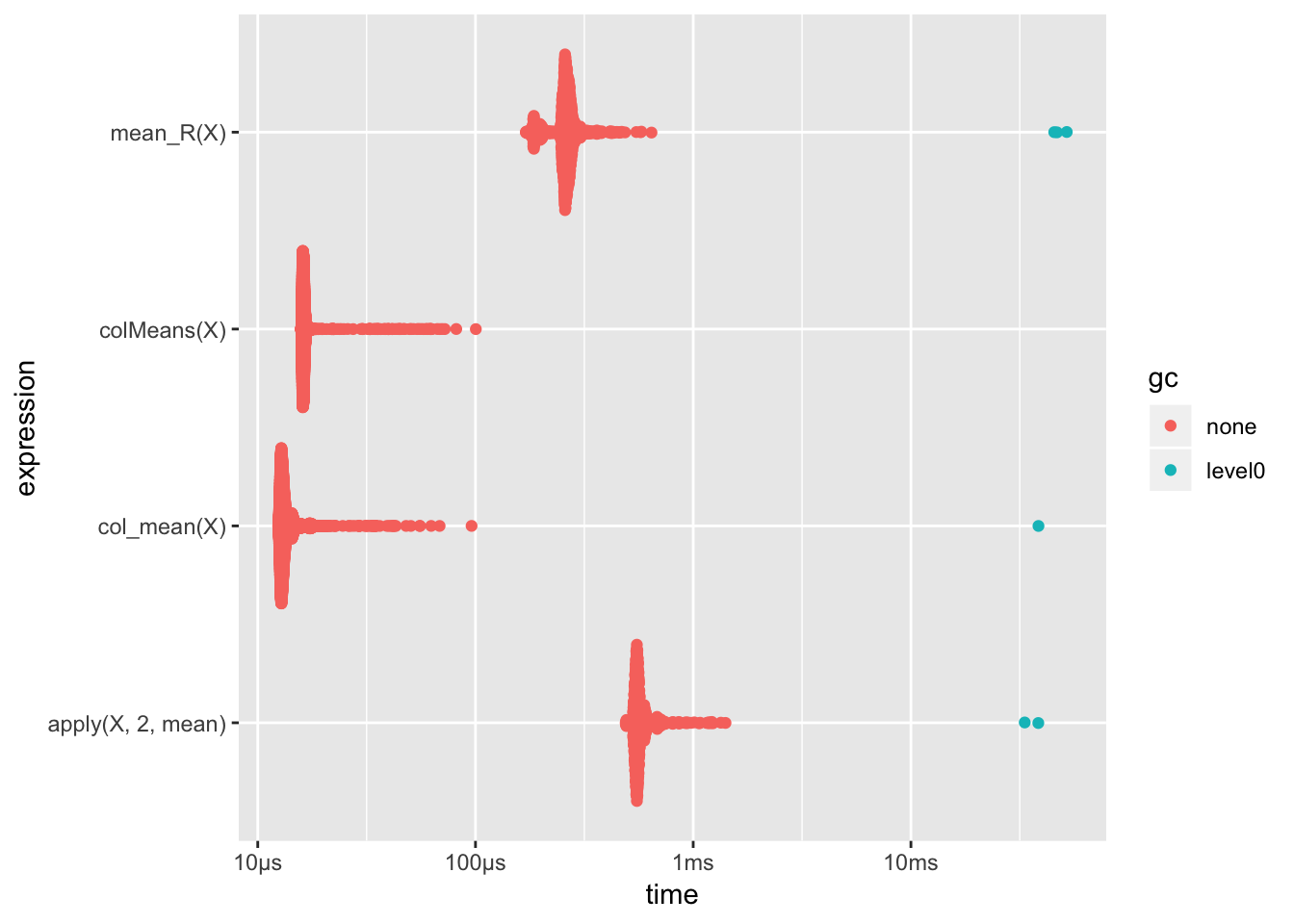

对比结果如图所示,其中gc¹²是一个关于内存使用的指标,越低越好.

apply和在R中用循环编写函数速度差不多,用C++编写的函数明显比其他快,甚至比base库中的函数还要快.不过,当我们增加矩阵的大小时,就会发现不一样的结果:

Rcpp::sourceCpp('code/Rcpp-demo.cpp')

## 
## > mean_R <- function(X) {
## +     n = dim(X)[1]
## +     m = dim(X)[2]
## +     cm <- rep(0, m)
## +     for (i in 1:n) {
## +         cm = cm + X[i, ]
## +     }
## +    .... [TRUNCATED]

m = 2000
n = 1000
X <- matrix(rnorm(m*n),m,n)
col_mean(X) -> l1
mean_R(X) -> l2
all.equal(l1,l2)

## [1] TRUE

colMeans(X) -> l3
all.equal(l1,l3)

## [1] TRUE

apply(X, 2, mean) -> l4
all.equal(l1,l4)

## [1] TRUE

bench::mark(
  col_mean(X),
  colMeans(X),
  mean_R(X),
  apply(X, 2, mean),
  check = FALSE,relative = TRUE
)->results
ggplot2::autoplot(results)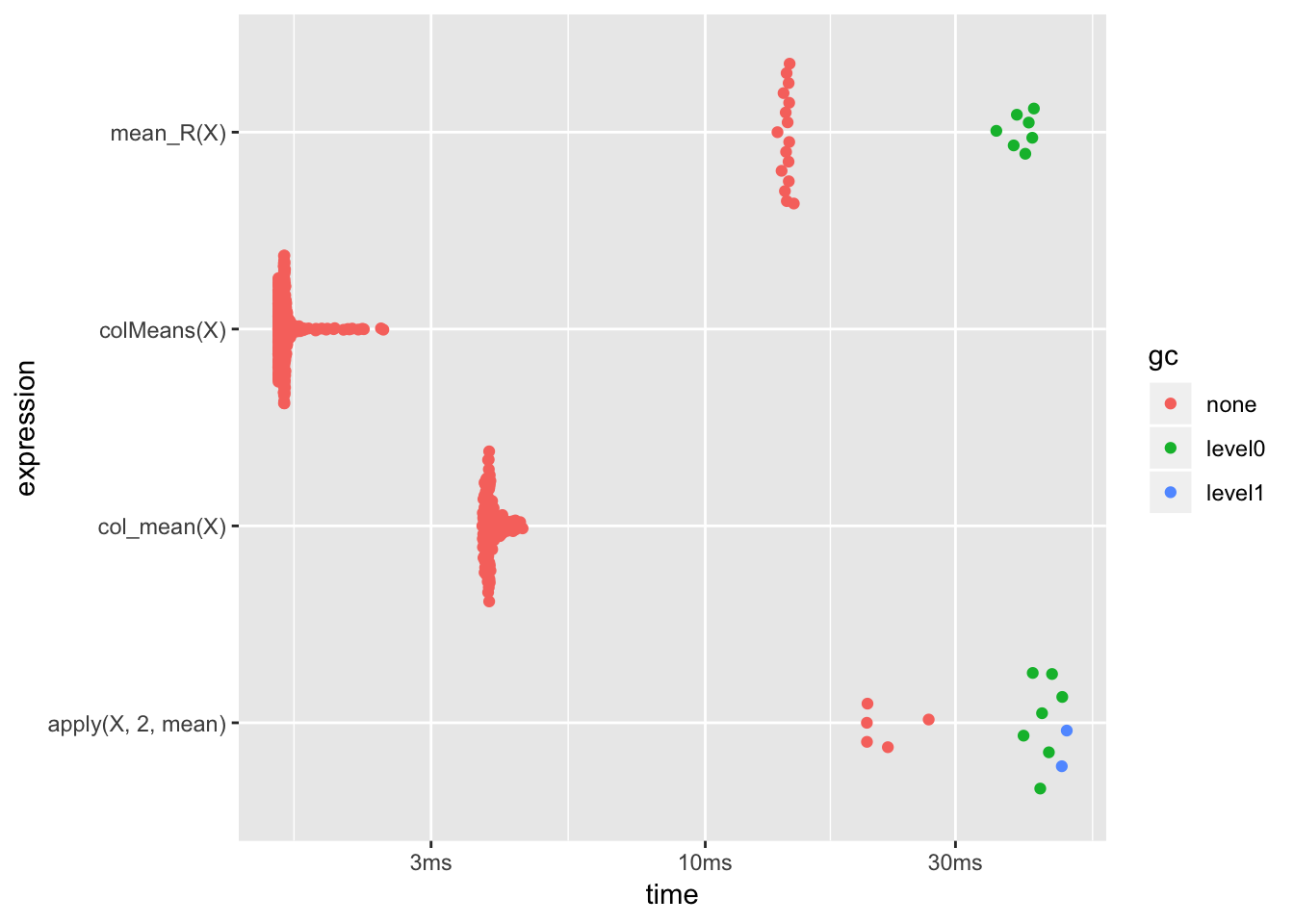

可以看到,还是base库中提供的函数速度最快.

4.3.1 RcppParallel

C++并行库

官方文档

这里提供一个RcppParallel的例子: 核估计

下面是三个关于线性代数的库,https://gist.github.com/wolfv/ca3ac2b24e1daf70f85eac18ec7b1b8f 这个例子的测试结果表明xtensor最快

4.3.2 RcppArmadillo

线性代数库官方文档

4.3.3 RcppEigen

线性代数库(更快一点,但是不友好) 官方文档

4.3.4 xtensor

GitHub地址

程序在这里查看,其中最后被/***R */夹住的部分是R程序,每次加载后会自动执行,方便调试.↩
垃圾回收（英语：Garbage Collection，缩写为GC），在计算机科学中是一种自动的存储器管理机制。当一个计算机上的动态存储器不再需要时，就应该予以释放，以让出存储器，这种存储器资源管理，称为垃圾回收。↩

第 4 章 进阶技巧