第 3 章 假设检验

假设检验部分模拟相对简单,只需要在估计出参数值后,按照检验统计量的形式正确计算即可.主要难点在于构造检验统计量以及给出检验统计量的渐近分布.

常用的办法是通过自助法(bootstrap)估计分布.

我们以最简单的二项分布为例,说明一些假设检验中的概念.

X	p=0.5	p=0.6	p=0.7	p=0.8	p=0.9
0	0.0010	0.0001	0.0000	0.0000	0.0000
1	0.0098	0.0016	0.0001	0.0000	0.0000
2	0.0439	0.0106	0.0014	0.0001	0.0000
3	0.1172	0.0425	0.0090	0.0008	0.0000
4	0.2051	0.1115	0.0368	0.0055	0.0001
5	0.2461	0.2007	0.1029	0.0264	0.0015
6	0.2051	0.2508	0.2001	0.0881	0.0112
7	0.1172	0.2150	0.2668	0.2013	0.0574
8	0.0439	0.1209	0.2335	0.3020	0.1937
9	0.0098	0.0403	0.1211	0.2684	0.3874
10	0.0010	0.0060	0.0282	0.1074	0.3487

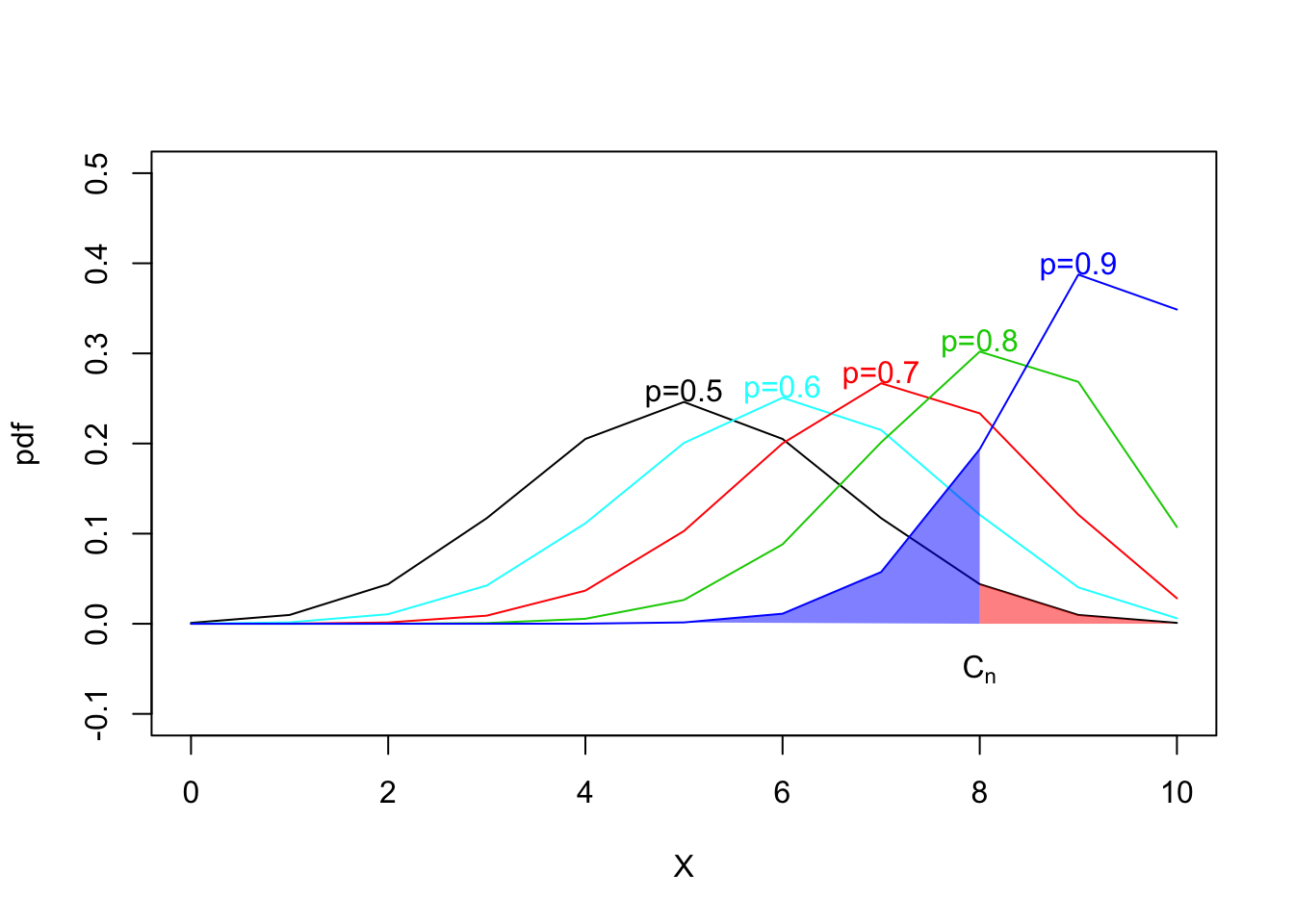
显著水平=第一类错误=\(\alpha\):为图中红色区域的面积

第二类错误=\(\beta\):为图中蓝色区域的面积

功效=势=power=\(1- \beta\):为图中蓝色曲线下空白面积

检验的相合性:

1. 在\(H_0\)下, 拒绝概率(size)收敛到\(\alpha.\)
2. 在\(H_1\)下, 拒绝概率(power)收敛到\(1.\)